نظام إحداثي ديكارتي

في الرياضيات، يستعمل نظام الإحداثيات الديكارتية لتحديد نقطة في مستوي عبر عددين، يطلق عليهما عادة الإحداثية-س والإحداثية-ص. لتعريف الإحداثيات، نقوم بإسقاط خطين عموديين (محور السينات أو س ومحور الصادات أو ص)، كما يجب كذلك تعريف وحدة الطول، والتي نبيّنها على المحورين (انظر الصورة 1).
تستعمل أنظمة الإحداثيات الديكارتية في الفضاء أيضا (باستعمال ثلاث إحداثيات)، أو حتى في أبعاد أكثر.
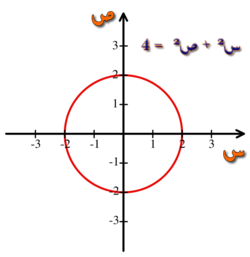
باستعمال نظام الإحداثيات الديكارتية، يمكن التعبير عن الأشكال الهندسية باستعمال معادلات جبرية، وهي معادلات توافق إحداثيات النقاط الممثّلة للشكل الهندسي. فعلى سبيل المثال، يعبّر عن دائرة ذات شعاع مساو لـ2، بالمعادلة التالية س² + ص² = 4. (انظر الصورة 2).
سمي النظام بالـديكارتي تبعا للرياضي والفيلسوف الفرنسي ريني ديكارت (كارتيسيوس باللاتينية)، والذي عمل على ادماج الجبر والهندسة الإقليدية. كان هذا العمل حاسما في مجال الهندسة التحليلية ودراسة الدوال والخرائط.
تم تطوير فكرة النظام هذه سنة 1637، في كتابتين مختلفتين لديكارت. في الجزء الثاني من حديث الطريقة، يقدّم ديكارت فكرته الجديدة لتحديد موقع نقطة أو شكل على المستوي، باستعمال محورين متقاطعين كآداة للقياس. وفي الهندسة، يكشف ديكارت أكثر عن المفاهيم التي سبق ذكرها.
نظام الإحداثيات ثنائي الأبعاد



يعرّف نظام الإحداثيات الديكارتي الحديث ذو البعدين عادة بمحورين، يشكلان مستو (مستوي-س،ص). يعنون المحور الأفقي عادة بـ س، والعمودي بـ ص. أما في النظام ذو الأبعاد الثلاث، يتم إضافة محور ثالث، يسمى عادة ز، مما يضيف بعدا ثالثا للقياس. تختار المحاور عادة متعامدة بعضها مع بعض. تسمى المعادلات التي تستخدم الإحداثيات الديكارتية، معادلات ديكارتية.
يسمى تقاطع المحاور، بالنقطة الأصل وتسمى عادة م. يحدد محوري السينات والصادات مستو يعرف بمستوى السينات-الصادات. كما يجب اختيار وحدة طول، والإشارة إليها على المحورين، لتشكيل شبكة. لتحديد نقطة ما في نظام ديكارتي ثنائي الأبعاد، حدد إحداثية السين أولا (س) ثم إحداثية الصاد (ص) في شكل زوج مرتّب (س،ص).
على سبيل المثال النقطة أ في الصورة 3، باستعمال الإحداثيات (5،3).
يحدد تقاطع المحورين أربع مناطق، يشار إليها بالأرقام الرومانية I (+,+) وII (−,+) وIII (−,−) وIV (+,−). اتفاقا، ترقم هذه المناطق عكس عقارب الساعة ابتداءا من المنطقة اليمنى العليا. في المنطقة الأولى، تكون كلا الإحداثيتين موجبتين، أما في الثانية، فتكون إحداثية السين سالبة وإحداثية الصاد موجبة، أما في المنطقة الثالثة تكون كلاهما سالبتين، وأخيرا في المنطقة الرابعة تكون إحداثية السين موجبة وإحداثية الصاد سالبة.(انظر الصورة 3).
نظام الإحداثيات ثلاثي الأبعاد
يوفّر نظام الإحداثيات ثلاثي الأبعاد، الأبعاد الفيزيائية الثلاث : الطول، العرض، الارتفاع. تبيّن الصورتان 4 و5، طريقتين معتمدتين لعرض نظام إحداثيات ثلاثي الأبعاد.
تكون الإحداثيات في النظام الثلاثي الأبعاد على شاكلة (س،ص،ع). وعلى سبيل المثال، تم تصوير نقطتين في نظام الصورة 4، النقطة أ(3،0،5) والنقطة ب(-5،-5،7).
يمكن كذلك استنتاج إحداثيات الس، والص، والع من الأبعاد عن المستوي ص، ع والمستوي س،ع والمستوي س،ص. تبيّن الصورة 5 أبعاد النقطة أ عن المستويات.
تقسّم محاور النظام الثلاثي الأبعاد الفضاء إلى ثمان مناطق شبيهة بمناطق النظام ثنائي الأبعاد.
في الفيزياء
ينطبق ما سبق على نظام الإحداثيات الديكارتية في الرياضيات، حيث من العادي أن لا تستعمل أي وحدة للقيس. ولكن، من الضروري أن نؤكد أن الأبعاد في الفيزياء هي ببساطة قيس لشيء ما، وأنه قد يكون من الضروري أيضا إضافة بعد آخر. إن الأشياء متعددة-الأبعاد يمكن أن نحسبها ونتحكم بها جبريا.
تمثيل متّجه بكتابات ديكارتية
يمكن كذلك التعبير عن نقطة في نظام إحداثيات ديكارتي بمتجه، الذي يمكن تصويره على أنه سهم منطلق من النقطة الأصل ومشير إلى تلك النقطة. إذا كانت الإحداثيات تعبّر عن مواقع فضائية، من المتعارف عليه تصوير المتجه من الأصل إلى النقطة بـ . وباستعمال الإحداثيات الديكارتية يكتب المتجه من الأصل إلى النقطة :
حيث و و هي متجهات وحدة تشير إلى نفس اتجاهات محاور الـ و و، على الترتيب.
انظر أيضا
af:Cartesiese koördinatestelsel bg:Декартова координатна система bn:কার্তেসীয় স্থানাংক ব্যবস্থা bs:Descartesov koordinatni sistem ca:Sistema de coordenades cartesianes cs:Kartézská soustava souřadnic da:Kartesisk koordinatsystem de:Kartesisches Koordinatensystem el:Καρτεσιανό σύστημα συντεταγμένων en:Cartesian coordinate system eo:Kartezia koordinato es:Coordenadas cartesianas fa:دستگاه مختصات دکارتی fi:Koordinaatisto#Suorakulmainen koordinaatisto fr:Coordonnées cartésiennes he:מערכת צירים קרטזית hi:कार्तीय निर्देशांक पद्धति hy:Դեկարտյան կոորդինատների համակարգ id:Sistem koordinat Kartesius is:Kartesíusarhnitakerfið it:Sistema di riferimento cartesiano ja:直交座標系 ko:직교 좌표계 lv:Dekarta koordinātu sistēma mr:कार्टेशियन गुणक पद्धती ms:Sistem koordinat Cartes nds:Karteesch Koordinatensystem nl:Cartesisch coördinatenstelsel nn:Kartesisk koordinatsystem no:Kartesisk koordinatsystem pl:Układ współrzędnych kartezjańskich pt:Sistema de coordenadas cartesiano ro:Coordonate carteziene ru:Прямоугольная система координат scn:Sistema di rifirimentu cartisianu sh:Kartezijanski koordinatni sistem simple:Cartesian coordinate system sk:Karteziánska sústava súradníc (v najužšom zmysle) sl:Kartezični koordinatni sistem sq:Sistemi koordinativ kartezian sr:Декартов координатни систем sv:Kartesiskt koordinatsystem ta:காட்டீசியன் ஆள்கூற்று முறைமை th:ระบบพิกัดคาร์ทีเซียน tr:Kartezyen koordinat sistemi uk:Декартова система координат ur:Cartesian coordinate system vi:Hệ tọa độ Descartes zh:笛卡儿坐标系